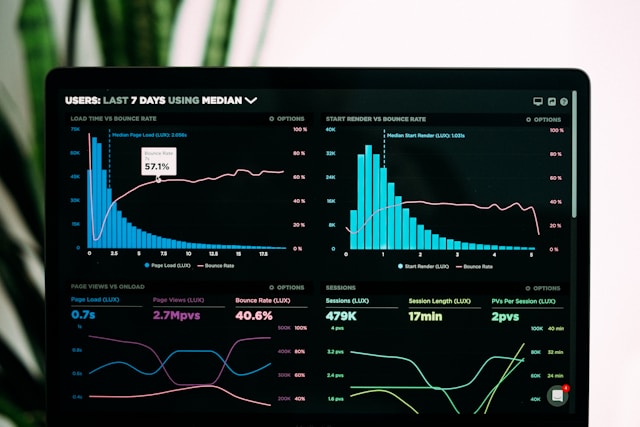
目次
邪馬台国研究に訪れた方法論の転換点
季刊『邪馬台国』第146号は、邪馬台国論争の歴史において、明確な指針を示す号であると言ってよい。本号で安本美典氏が挑戦しているのは、邪馬台国の所在地を「どこだと思うか」という主観的判断から切り離し、「どこにあった可能性がどれほど高いのか」を数理的かつ確率的に評価することである。そこに導入されているのが、データサイエンス、とりわけベイズ統計という思考枠組みだ。
従来の議論では、魏志倭人伝の解釈や考古学的印象評価が中心となり、議論はしばしば平行線をたどってきた。第146号は、その膠着状態に対し、「議論の土俵そのものを変える」という戦略をとる。感覚ではなく確率、印象ではなく数値、権威ではなく再現可能な計算。その姿勢が全編を貫いている。
勾玉データが示す「偏り」という事実
本号の分析の起点となるのが、勾玉の県別出土数である。勾玉は弥生時代において、明確に権威性を帯びた遺物であり、その分布は政治的中枢の存在と強く結びつく。誌面では、硬玉製勾玉を中心に、出土数を県別に整理し、その分布の「偏り」を定量的に示している。

結果はきわめて明瞭だ。福岡県の出土数は、奈良県を含む他地域を圧倒している。この事実自体は、考古学者の間でも知られていたが、本号の特徴は、それを「印象」ではなく「確率計算の前提データ」として扱う点にある。つまり、「多いか少ないか」ではなく、「この差が偶然で生じる確率はどれほどか」を問うのである。
ベイズ統計とは何か、なぜ有効なのか
ここで登場するのがベイズ統計である。ベイズの定理は、結果から原因を推定するための数学的道具であり、次の式で表される。
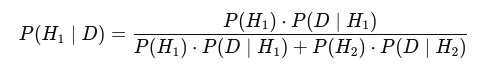
ベイズの定理ってなに?それは結果から原因を推定する確率論。
- (H) は仮説、(P(H)) は仮説 (H) が正しいと考える事前確率と呼ばれる。
- (D) はデータ、(P(D | H)) は「仮説 (H) が正しいときに、データ (D) が得られる確率」を表す。
- (P(H | D)) は「データ (D) が与えられたときに、仮説 (H) が正しい確率」を意味する。
つまり、
仮説は仮説であり、データが与えられた時に、仮説が正しい確率を計算する
のがベイズの定理である。例えば、「邪馬台国が福岡県にあるという仮説」をベイズの定理によって検定するとすると、
Hは仮説、Dは観測データ、つまり
H:あくまで仮説 → 邪馬台国は福岡県にあった
D:勾玉・鉄鏃・鏡などが福岡県に集中して出土している(具体的な出土数)
という関係である。P(H|D)は「データを見た後で、その仮説が正しい確率」を表す。重要なのは、ベイズ統計では「新しいデータが加わるたびに、仮説の確率を更新できる」という点だ。これは歴史研究において極めて相性がよい。
第146号では、この式を抽象論に終わらせず、実際の出土数を用いて計算を行っている。結果は劇的である。福岡県説の事後確率は99%以上、奈良県説は0.1%以下という数値が導かれる。この差は直感の問題ではなく、計算結果として示される。
奈良邪馬台国説は終焉していることが統計的に示される。

複数指標の掛け算が意味するもの
本号の分析が説得力を持つ理由は、勾玉だけに依存していない点にもある。鉄鏃、鏡、絹といった複数の考古指標を独立したデータとして扱い、それらを掛け合わせて総合評価を行っている。これはデータサイエンスにおける特徴量統合そのものである。
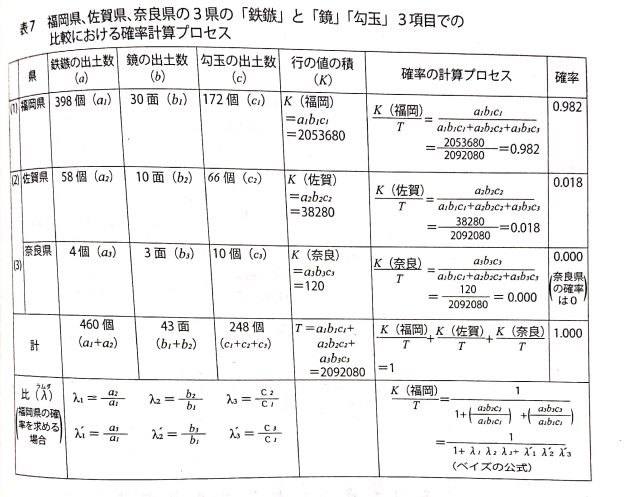
仮に一つの指標に偏りがあっても、別の指標がそれを補正する。しかし福岡県の場合、すべての指標で高い値を示すため、掛け算によって他地域との差はむしろ拡大する。この構造は、恣意的なデータ選択という批判を根本から無効化する。
邪馬台国論争の先に見えるもの
季刊『邪馬台国』第146号が示しているのは、邪馬台国北部九州説の優位性だけではない。より重要なのは、「歴史学はどのように検証されうるのか」という問いへの一つの答えである。数式は歴史を冷たくするのではなく、むしろ議論を公平にする。
この号を読み終えたとき、読者は邪馬台国の所在地以上に、「歴史研究における方法論の未来」を考えさせられるだろう。感覚や信念ではなく、データと確率で語る古代史。その可能性を具体的に示したという点で、第146号は邪馬台国探索者には必読の一冊である。